Rosetta store: contrasts

keywords jamovi, SPSS, R, contrasts, comparisons, planned comparisons, LMATRIX, contr.sum, emmeans

0.9.5

Introduction

Here you can find comparisons of results obtained in GAMLj, jamovi (jmv), pure R, and SPSS. When not explicitely discussed, the code of different software is written with the aim of obtaing identical results across programs.

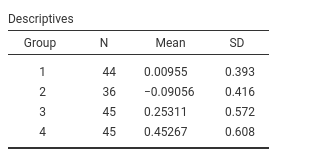
Example data are here or in the jamovi data library, under General Analysis for Linear Models (3), named fivegroups. One continuous dependent variable, one factor with 4 groups.

Unfortunately, contrasts coding schemes get different names in different publications and they are implemented in different ways across software. Things can get a bit confusing because of this. For partially overlapping coding scheme definitions see UCLA idre web site, SPSS manual and Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2013). Applied multiple regression/correlation analysis for the behavioral sciences. Routledge. If you have familiarity with python, you can compare results also with python statmodels results

Software

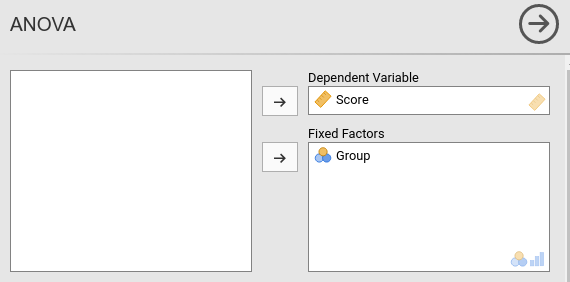
We use jamovi, SPSS and R. In jamovi we compare the ANOVA module in jamovi jmv and the GAMLj module. In R we use pure R, meaning that we estimate the contrast comparisons by estimating a linear model (lm() in particular), with the categorical variable properly coded. For more straigthforward estimation we employ emmeans R module. In SPSS we use the UNIVARIATE module.

More technical details

Contrasts can be computed in two different ways:

  • As the coefficients of a model where the categorical variable(s) is coded accordingly to a coding scheme. jamovi GAMLj and standard R use this strategy. Understanding this approach opens to the possibility to test contrasts-based hypotheses in complex models, such as when interactions are involved, mediatiated effects or simple effects are of interest.

  • As a comparison between sets of means tested with model-derived standard errors. jamovi ANOVA, emmeans R and SPSS use this approach. This approach is simpler and straightforward. In simple models, it works perfectly fine.

  • As a comparison between groups means, with group specific standard errors. None of the software used here uses this approach, so we do not deal with it here.

The first two approaches give the same results if the contrasts are defined in the same way. However, the contrast coding displayed by the software may be different. The majority of software prints out the contrast matrix, which contains the coding scheme describing the tested comparisons. R model estimation requires the model matrix, which is generally different from the contrast matrix and represents the weights associated with the dummy variables needed to cast a categorical variable into the linear model estimating the contrasts. How they are related and how to obtain one from the other is explained in contrast vs model matrix details

Furthermore, in simple models (such as one-way ANOVA), the two first approaches give exactly the same results. When models get more complex, results may diverge across software because they estimate different things. The present results apply to one-way ANOVA, balanced factorial ANOVA with centered coding scheme, ANCOVA models with continuous covariates centered to their means.

Terminology

To interpret a contrast, it is often necessary to refer to “the first group” or “subsequent groups”. The order is always defined as the alphanumeric order.

Furthermore, different software packages have different rounding rules, so we say “the same results” when results agree apart for decimal rounding.

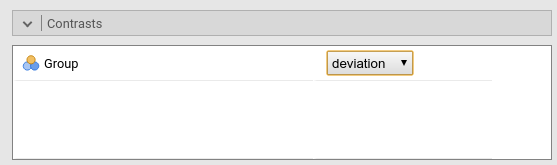
Contrast: Deviation

Meaning

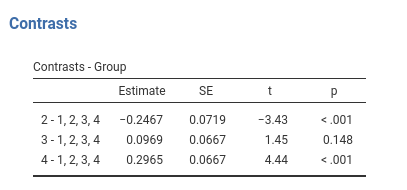
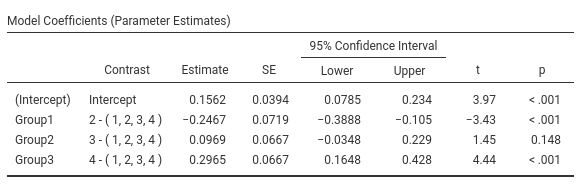
Definition: Compares each group mean to the grand mean. The grand mean is the mean of the groups means. The first group is omitted

jamovi ANOVA

Setting the contrasts to deviation

Results:

jamovi GAMLj GLM

Results:

The expected means of the four groups are:

SPSS

Please note that SPSS default sets the last group as reference group (the omitted group), thus to obtain the same results as before, we should set /CONTRAST(Group)=Deviation(1), mind the “1”“, which corresponds to”first” in the GUI options.

UNIANOVA Score BY Group
  /CONTRAST(Group)=Deviation(1)
  /METHOD=SSTYPE(3)
  /INTERCEPT=INCLUDE
  /PRINT=TEST(LMATRIX)
  /CRITERIA=ALPHA(.05)
  /DESIGN=Group.

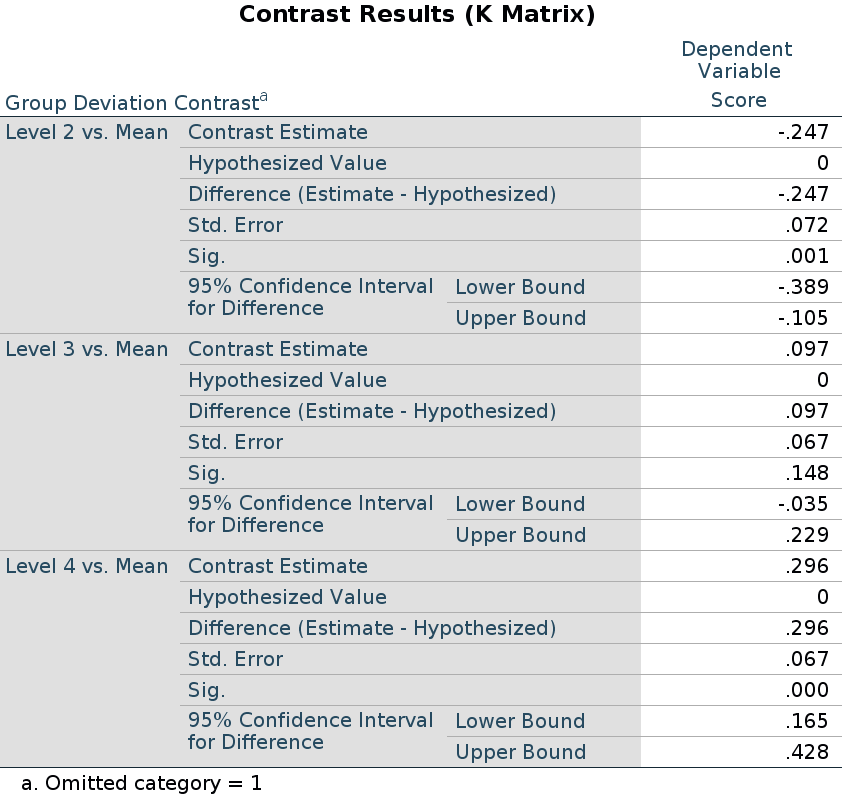
R

In R, deviation contrast is called contr.sum. The function defaults to omitting the last group, so we reverse it to omit the first.

file<-"../data/rosetta.contrasts.csv"
dat<-read.csv2(file,stringsAsFactors = F)
dat$Group<-factor(dat$Group)
dat$Score<-as.numeric(dat$Score)
### reverse contrast sum ###
contrasts(dat$Group)<-matrix(rev(contr.sum(4)),ncol=3)
contrasts(dat$Group)
##   [,1] [,2] [,3]
## 1   -1   -1   -1
## 2    1    0    0
## 3    0    1    0
## 4    0    0    1
model<-lm(Score~Group,data=dat)
summary(model)
## 
## Call:
## lm(formula = Score ~ Group, data = dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.06311 -0.27955 -0.00111  0.28531  1.65733 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.15619    0.03936   3.969 0.000107 ***
## Group1      -0.24675    0.07193  -3.430 0.000760 ***
## Group2       0.09692    0.06670   1.453 0.148092    
## Group3       0.29647    0.06670   4.445 0.000016 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5109 on 166 degrees of freedom
## Multiple R-squared:  0.1473, Adjusted R-squared:  0.1319 
## F-statistic: 9.557 on 3 and 166 DF,  p-value: 0.000007399
## means
(mm<-tapply(dat$Score, dat$Group, mean))
##            1            2            3            4 
##  0.009545455 -0.090555556  0.253111111  0.452666667

R emmeans

To employ emmeans package, we first estimate the model (which coding system we use does not matter), then we run the function emm<-emmeans(model,specs), where specs is the factor for which we want to compare the means, and then we apply contrast(emm,contrast_type) to the emmeans object. contrast_type is a string equal to the contrast function we want to use. We add adjust="none" to obtain the same p-values as in the previous analyses, but any adjustment supported by emmeans can be applied here. If we omit the adjust option, the default multiplicity adjustment method is “fdr” , cf. emmeans package.

The deviation contrast it is named eff in emmeans.

library(emmeans)
model<-lm(Score~Group,data=dat)
emm<-emmeans(model,~Group)
contrast(emm,"eff",reverse=T,adjust = "none")
##  contrast      estimate     SE  df t.ratio p.value
##  Group1 effect  -0.1466 0.0672 166  -2.183  0.0305
##  Group2 effect  -0.2467 0.0719 166  -3.430  0.0008
##  Group3 effect   0.0969 0.0667 166   1.453  0.1481
##  Group4 effect   0.2965 0.0667 166   4.445  <.0001

Please notice that emmeans computes all possible comparisons: group 1 against the grand mean, group 2 against the grand mean, etc.

Contrast: Simple & Dummy

Meaning

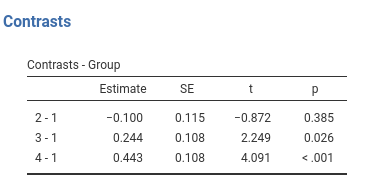
Definition: Compares each group with the first group.

jamovi ANOVA

We set the contrasts to simple

Results:

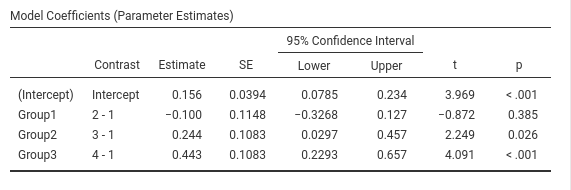
jamovi GAMLj GLM

This is GAMLj default (since version 1.5). The contrasts in GAMLj is identical to the ANOVA module.

SPSS

Please note that SPSS default sets the last group as reference group, thus to obtain the same results as before, we should set /CONTRAST(Group)=Simple(1), mind the “1”“, which corresponds to”first” in the GUI options.

UNIANOVA Score BY Group
  /CONTRAST(Group)=Simple(1)
  /METHOD=SSTYPE(3)
  /INTERCEPT=INCLUDE
  /PRINT=TEST(LMATRIX)
  /CRITERIA=ALPHA(.05)
  /DESIGN=Group.

Results:

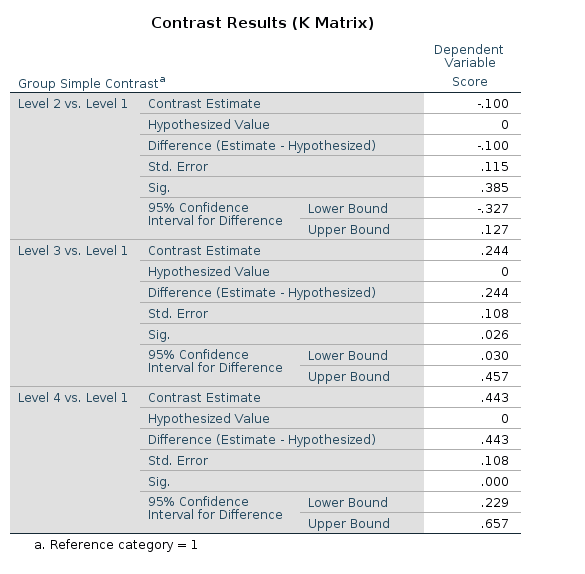
R

In R, simple contrast can be obtained as follows:

#### contrast=simple #######
dat$Group<-factor(dat$Group)
k<-4 # number of levels
contrasts(dat$Group)<-contr.treatment(k)-(1/k)
contrasts(dat$Group)
##       2     3     4
## 1 -0.25 -0.25 -0.25
## 2  0.75 -0.25 -0.25
## 3 -0.25  0.75 -0.25
## 4 -0.25 -0.25  0.75
model<-lm(Score~Group,data=dat)
summary(model)
## 
## Call:
## lm(formula = Score ~ Group, data = dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.06311 -0.27955 -0.00111  0.28531  1.65733 
## 
## Coefficients:
##             Estimate Std. Error t value  Pr(>|t|)    
## (Intercept)  0.15619    0.03936   3.969  0.000107 ***
## Group2      -0.10010    0.11481  -0.872  0.384538    
## Group3       0.24357    0.10831   2.249  0.025846 *  
## Group4       0.44312    0.10831   4.091 0.0000668 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5109 on 166 degrees of freedom
## Multiple R-squared:  0.1473, Adjusted R-squared:  0.1319 
## F-statistic: 9.557 on 3 and 166 DF,  p-value: 0.000007399

If one need the uncentered dummy coding, it can be obtained in R using contr.treatment(k).

R emmeans

The simple contrast can be achieved in emmeans with dunnett.

model<-lm(Score~Group,data=dat)
emm<-emmeans(model,~Group)
contrast(emm,"dunnett",adjust = "none")
##  contrast        estimate    SE  df t.ratio p.value
##  Group2 - Group1   -0.100 0.115 166  -0.872  0.3845
##  Group3 - Group1    0.244 0.108 166   2.249  0.0258
##  Group4 - Group1    0.443 0.108 166   4.091  0.0001

Simple vs Dummy

GAMLj distinguishes between simple and dummy coding schemes. They give equivalent results in means comparisons, simple effects, and contrast coefficients. The only difference is that the Dummy is not centered, and so when the codes are involved in interactions, the effects of the other variables have different meaning. In the presence of interactions, when simple is used, the other variables effects are computed averaging across the sample; when dummy is used, the other variables effects are computed for the reference group (the first group) defined by the dummy coding.

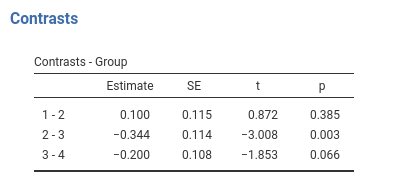
Contrast: Repeated

Definition: Compares each group with the subsequent group

jamovi ANOVA

Results:

jamovi GAMLj GLM

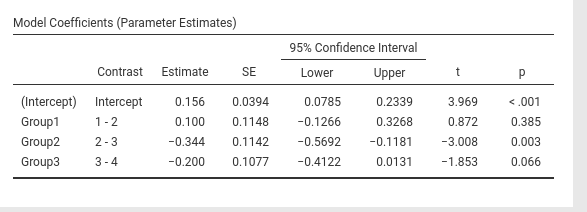
SPSS

UNIANOVA Score BY Group
  /CONTRAST(Group)=REPEATED
  /METHOD=SSTYPE(3)
  /INTERCEPT=INCLUDE
  /PRINT=TEST(LMATRIX)
  /CRITERIA=ALPHA(.05)
  /DESIGN=Group.

R

R does not have an out-of-the-box contrast equivalent to repeated contrast. One can, howerver, uses the contr.sdif() function in MASS package. As compared with jamovi and SPSS the comparisons are in the opposite direction, so we simply multiply the code by -1 (t-tests and p-values do not depend on this):

library(MASS)
repeated<-(-1)*contr.sdif(4) 
repeated
##     2-1  3-2   4-3
## 1  0.75  0.5  0.25
## 2 -0.25  0.5  0.25
## 3 -0.25 -0.5  0.25
## 4 -0.25 -0.5 -0.75
contrasts(dat$Group)<-repeated
summary(lm(Score~Group,data=dat))
## 
## Call:
## lm(formula = Score ~ Group, data = dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.06311 -0.27955 -0.00111  0.28531  1.65733 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.15619    0.03936   3.969 0.000107 ***
## Group2-1     0.10010    0.11481   0.872 0.384538    
## Group3-2    -0.34367    0.11424  -3.008 0.003036 ** 
## Group4-3    -0.19956    0.10770  -1.853 0.065681 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5109 on 166 degrees of freedom
## Multiple R-squared:  0.1473, Adjusted R-squared:  0.1319 
## F-statistic: 9.557 on 3 and 166 DF,  p-value: 0.000007399

… and we’re just fine.

R emmeans

The repeated contrast can be achieved in emmeans with consec. To align the results to the jamovi SPSS, we should reverse the contrast coding, with the option reverse.

model<-lm(Score~Group,data=dat)
emm<-emmeans(model,~Group)
contrast(emm,"consec",adjust = "none",reverse=T)
##  contrast        estimate    SE  df t.ratio p.value
##  Group1 - Group2    0.100 0.115 166   0.872  0.3845
##  Group2 - Group3   -0.344 0.114 166  -3.008  0.0030
##  Group3 - Group4   -0.200 0.108 166  -1.853  0.0657

Contrast: Polynomial

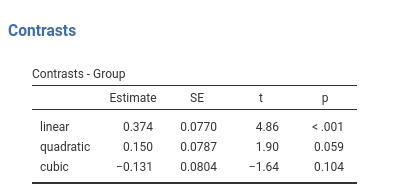
Definition: Test polynomial (linear, quadratic, cubic, etc.) trends in the means pattern

jamovi ANOVA

Results:

jamovi GAMLj GLM

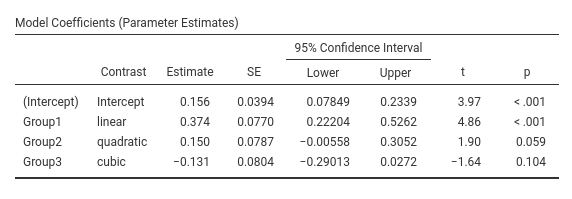
SPSS

UNIANOVA Score BY Group
  /CONTRAST(Group)=POLYNOMIAL
  /METHOD=SSTYPE(3)
  /INTERCEPT=INCLUDE
  /PRINT=TEST(LMATRIX)
  /CRITERIA=ALPHA(.05)
  /DESIGN=Group.

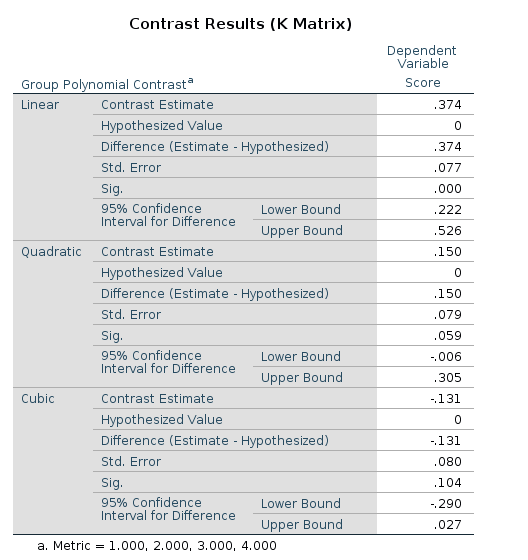
R

R has an out-of-the-box contrast named contr.poly() contrast. It works like a sharm.

contrasts(dat$Group)<-contr.poly(4)
summary(lm(Score~Group,data=dat))
## 
## Call:
## lm(formula = Score ~ Group, data = dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.06311 -0.27955 -0.00111  0.28531  1.65733 
## 
## Coefficients:
##             Estimate Std. Error t value   Pr(>|t|)    
## (Intercept)  0.15619    0.03936   3.969   0.000107 ***
## Group.L      0.37410    0.07702   4.857 0.00000273 ***
## Group.Q      0.14983    0.07871   1.904   0.058702 .  
## Group.C     -0.13145    0.08037  -1.636   0.103809    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5109 on 166 degrees of freedom
## Multiple R-squared:  0.1473, Adjusted R-squared:  0.1319 
## F-statistic: 9.557 on 3 and 166 DF,  p-value: 0.000007399

… and we can sleep like babies.

R emmeans

The poly contrast has a direct implementation in emmeans with poly.

model<-lm(Score~Group,data=dat)
emm<-emmeans(model,~Group)
contrast(emm,"poly",adjust = "none")
##  contrast  estimate    SE  df t.ratio p.value
##  linear       1.673 0.344 166   4.857  <.0001
##  quadratic    0.300 0.157 166   1.904  0.0587
##  cubic       -0.588 0.359 166  -1.636  0.1038

Contrast: Difference

Difference and helmert contrasts are great source of confusion when one is comparing different software results. SPSS and jamovi use the same definition for them, but R has a different implementation. Different authors uses different definitions, so be aware of which comparisons are implemented.

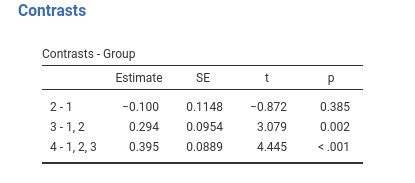
Definition: Compares each group with the average of previous groups.

This is sometimes named Reverse Helmert Coding , cf. UCLA idre web site.

jamovi ANOVA

Results:

jamovi GAMLj GLM

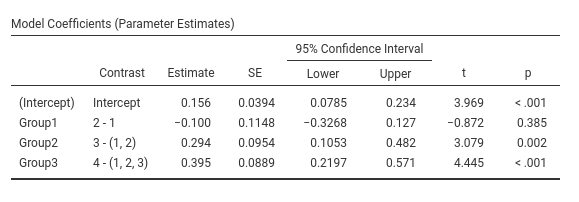
SPSS

UNIANOVA Score BY Group
  /CONTRAST(Group)=DIFFERENCE
  /METHOD=SSTYPE(3)
  /INTERCEPT=INCLUDE
  /PRINT=TEST(LMATRIX)
  /CRITERIA=ALPHA(.05)
  /DESIGN=Group.

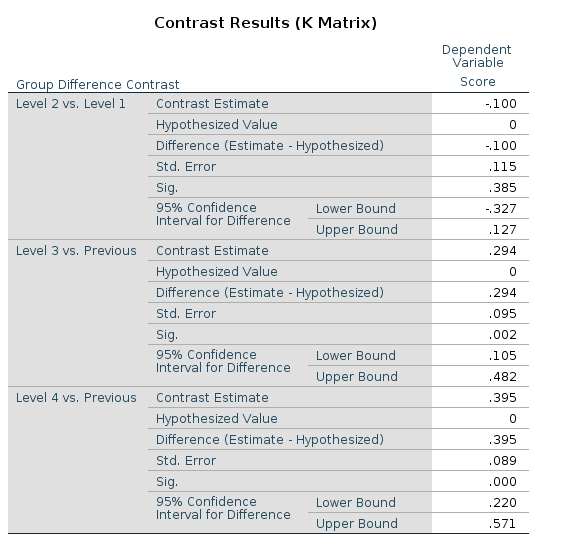
R

The t-tests and p-values associated with the difference contrast can be obtained in R using the contr.helmert() function. Despite the name, contr.helmert() implements what is usually named “Reversed Helmert contrast”. Obviously, this is perfectly fine (cf. An R and S-Plus Companion to Applied Regression), but one should be aware of this difference. The contrast weights in R are scaled differently than in SPSS or jamovi, thus the contrast values (the coefficients) are not identical to the ones obtained in jamovi and SPSS, but they are proportional to them (that is why the t-tests are the same).

dat$Group<-factor(dat$Group)
contrasts(dat$Group)<-contr.helmert(4)
contrasts(dat$Group)
##   [,1] [,2] [,3]
## 1   -1   -1   -1
## 2    1   -1   -1
## 3    0    2   -1
## 4    0    0    3
model<-lm(Score~Group,data=dat)
summary(model)
## 
## Call:
## lm(formula = Score ~ Group, data = dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.06311 -0.27955 -0.00111  0.28531  1.65733 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.15619    0.03936   3.969 0.000107 ***
## Group1      -0.05005    0.05741  -0.872 0.384538    
## Group2       0.09787    0.03179   3.079 0.002433 ** 
## Group3       0.09882    0.02223   4.445 0.000016 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5109 on 166 degrees of freedom
## Multiple R-squared:  0.1473, Adjusted R-squared:  0.1319 
## F-statistic: 9.557 on 3 and 166 DF,  p-value: 0.000007399

To obtain the jamovi/SPSS estimate values in R, we should multiply the coefficients obtained in R by the index of the column of the contrasts (starting from 2 because 1 is for the intercept). To make things a bit more general, we can define a conversion vector that works both for deviation and helmert contrasts. Let the conversion vector be \(\mathbf{cv}=max(c_i)+1\), where \(c_i\) is a column of the contrast matrix.

cv<-apply(contr.helmert(4),2,max)+1
cv
## [1] 2 3 4

To obtain the same coefficients in R and in jamovi/SPSS, we can multiply the model coefficients by \(\mathbf{cv}\)

coef(model)[c(2:4)]*cv
##     Group1     Group2     Group3 
## -0.1001010  0.2936162  0.3952997

Or divide the contrast weights by \(\mathbf{cv}\)

### make a diagonal matrix with cv in the diagonal ##########
diag_cv<-matrix(rep(cv,each=4),ncol=3)
contrasts(dat$Group)<-contr.helmert(4)/diag_cv
contrasts(dat$Group)
##   [,1]       [,2]  [,3]
## 1 -0.5 -0.3333333 -0.25
## 2  0.5 -0.3333333 -0.25
## 3  0.0  0.6666667 -0.25
## 4  0.0  0.0000000  0.75
model<-lm(Score~Group,data=dat)
summary(model)
## 
## Call:
## lm(formula = Score ~ Group, data = dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.06311 -0.27955 -0.00111  0.28531  1.65733 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.15619    0.03936   3.969 0.000107 ***
## Group1      -0.10010    0.11481  -0.872 0.384538    
## Group2       0.29362    0.09537   3.079 0.002433 ** 
## Group3       0.39530    0.08893   4.445 0.000016 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5109 on 166 degrees of freedom
## Multiple R-squared:  0.1473, Adjusted R-squared:  0.1319 
## F-statistic: 9.557 on 3 and 166 DF,  p-value: 0.000007399

… and we get the same values, t-tests and p-values as in jamovi and SPSS.

R emmeans

Difference and helmert are not implemented in emmeans package, but emmeans has a very clever way to implement custom contrast coding. We need to define a function whose name ends with .emmc and returns the coding as a data.frame, and then pass it to emmeans contrasts function. The coding weights are the one of the contrast matrix used in SPSS (see contrast matrix vs model matrix for details).

library(MASS) ## needed for ginv(), see below 

difference.emmc<<-function(levs,wts) {
  n<-length(levs)
  #### model matrix ########
  con_weights<-contr.helmert(n)
  cv<-apply(con_weights,2,max)+1
  diag_cv<-matrix(rep(cv,each=n),ncol=n-1)
  model_mat<-con_weights/diag_cv

  ##### contrast matrix ########
  cont_mat<-ginv(t(model_mat))
  M <- as.data.frame(cont_mat)
  names(M) <- paste(levs[-1],"vs previous")
  attr(M, "desc") <- "Difference contrasts"
  M
}
#### contrast matrix #########
round(difference.emmc(levels(dat$Group)),digits = 3)
##   2 vs previous 3 vs previous 4 vs previous
## 1            -1          -0.5        -0.333
## 2             1          -0.5        -0.333
## 3             0           1.0        -0.333
## 4             0           0.0         1.000
#### results ##############
contrast(emm,method="difference",adjust="none")
##  contrast           estimate     SE  df t.ratio p.value
##  Group2 vs previous   -0.100 0.1148 166  -0.872  0.3845
##  Group3 vs previous    0.294 0.0954 166   3.079  0.0024
##  Group4 vs previous    0.395 0.0889 166   4.445  <.0001

Same results as before.

Contrast: Helmert

Definition: Compares each group with the average of subsequent groups

jamovi ANOVA

Results:

jamovi GAMLj GLM

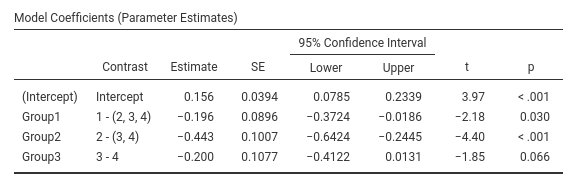
SPSS

UNIANOVA Score BY Group
  /CONTRAST(Group)=HELMERT
  /METHOD=SSTYPE(3)
  /INTERCEPT=INCLUDE
  /PRINT=TEST(LMATRIX)
  /CRITERIA=ALPHA(.05)
  /DESIGN=Group.

R

R defines helmert contrast in the reverse order as compared with jamovi and SPSS, and uses a different scaling. To obtain the helmert contrast as it is was defined above, we should reverse contr.helmert() and rescale the coding as we did for the difference contrasts. Without rescaling, the t-test and p-values are the same as in jamovi/spss, but the estimated values are different (but proportional).

dat$Group<-factor(dat$Group)
contrasts(dat$Group)<-matrix(rev(contr.helmert(4)),ncol=3)
con_weights<-contrasts(dat$Group)
#### not scaled contrast weights ######
con_weights
##   [,1] [,2] [,3]
## 1    3    0    0
## 2   -1    2    0
## 3   -1   -1    1
## 4   -1   -1   -1
model<-lm(Score~Group,data=dat)
summary(model)
## 
## Call:
## lm(formula = Score ~ Group, data = dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.06311 -0.27955 -0.00111  0.28531  1.65733 
## 
## Coefficients:
##             Estimate Std. Error t value  Pr(>|t|)    
## (Intercept)  0.15619    0.03936   3.969  0.000107 ***
## Group1      -0.04888    0.02240  -2.183  0.030477 *  
## Group2      -0.14781    0.03358  -4.402 0.0000192 ***
## Group3      -0.09978    0.05385  -1.853  0.065681 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5109 on 166 degrees of freedom
## Multiple R-squared:  0.1473, Adjusted R-squared:  0.1319 
## F-statistic: 9.557 on 3 and 166 DF,  p-value: 0.000007399

To obtain the jamovi/SPSS values in R, we should compute \(\mathbf{cv}=max(c_i)+1\), and multiply it by the model coefficients.

cv<-apply(con_weights,2,max)+1
cv
## [1] 4 3 2
coef(model)[c(2:4)]*cv
##     Group1     Group2     Group3 
## -0.1955286 -0.4434444 -0.1995556

or divide the contrast weights by \(\mathbf{cv}\)

### make a diagonal matrix with cv in the diagonal ##########
diag_cv<-matrix(rep(cv,each=4),ncol=3)
########  divide the contrast weights ##########
helm<-con_weights/diag_cv

### scaled contrast weights ############
helm
##    [,1]       [,2] [,3]
## 1  0.75  0.0000000  0.0
## 2 -0.25  0.6666667  0.0
## 3 -0.25 -0.3333333  0.5
## 4 -0.25 -0.3333333 -0.5
contrasts(dat$Group)<-helm
model<-lm(Score~Group,data=dat)
summary(model)
## 
## Call:
## lm(formula = Score ~ Group, data = dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.06311 -0.27955 -0.00111  0.28531  1.65733 
## 
## Coefficients:
##             Estimate Std. Error t value  Pr(>|t|)    
## (Intercept)  0.15619    0.03936   3.969  0.000107 ***
## Group1      -0.19553    0.08959  -2.183  0.030477 *  
## Group2      -0.44344    0.10075  -4.402 0.0000192 ***
## Group3      -0.19956    0.10770  -1.853  0.065681 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5109 on 166 degrees of freedom
## Multiple R-squared:  0.1473, Adjusted R-squared:  0.1319 
## F-statistic: 9.557 on 3 and 166 DF,  p-value: 0.000007399

… and we’re happy campers.

R emmeans

We need to define a funtion whose name ends with .emmc which returns the contrast matrix, and then pass it to emmeans contrasts. The contrast matrix is the same used in SPSS and can be obtained from the model matrix used in standard R (see contrast matrix vs model matrix for details).

library(MASS) # needed for ginv(), see below
helmert.emmc<<-function(levs, wts) {
  n<-length(levs)
  #### build model matricx ######
  con_weights<-matrix(rev(contr.helmert(n)),ncol=n-1)
  cv<-apply(con_weights,2,max)+1
  diag_cv<-matrix(rep(cv,each=n),ncol=n-1)
  model_mat<-con_weights/diag_cv
  #### obtain contrast matrix #######
  cont_mat<-ginv(t(model_mat))
  
  M <- as.data.frame(cont_mat)
  names(M) <- paste(levs[1:(length(levs)-1)],"vs subsequent")
  attr(M, "desc") <- "Helmert contrasts"
  M
}

helmert.emmc(levels(dat$Group))
##   1 vs subsequent            2 vs subsequent
## 1       1.0000000 -0.00000000000000006343273
## 2      -0.3333333  1.00000000000000000000000
## 3      -0.3333333 -0.50000000000000011102230
## 4      -0.3333333 -0.50000000000000011102230
##             3 vs subsequent
## 1 -0.0000000000000001098687
## 2 -0.0000000000000001256066
## 3  0.9999999999999995559108
## 4 -0.9999999999999997779554
contrast(emm,"helmert",adjust="none")
##  contrast             estimate     SE  df t.ratio p.value
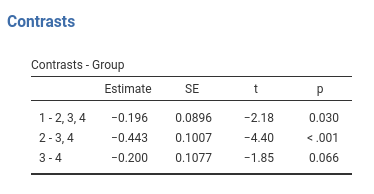
##  Group1 vs subsequent   -0.196 0.0896 166  -2.183  0.0305
##  Group2 vs subsequent   -0.443 0.1007 166  -4.402  <.0001
##  Group3 vs subsequent   -0.200 0.1077 166  -1.853  0.0657

Same results!

Contrast matrix vs model matrix

We have seen that jamovi, SPSS and emmeans provide descriptions of the comparisons being estimated as labels of the contrast. However, if one needs to deepen the understanding of the contrast at hand, one needs to examine the contrast coding scheme. SPSS and emmeans can show the coding scheme in the form of contrast matrix.

To visualize the contrast matrix in in SPSS one uses the option /PRINT=TEST(LMATRIX) , and in emmeans one can use the function coef() on the contrast object output by the contrast() function.

Let’s see an example using the repeated contrast:

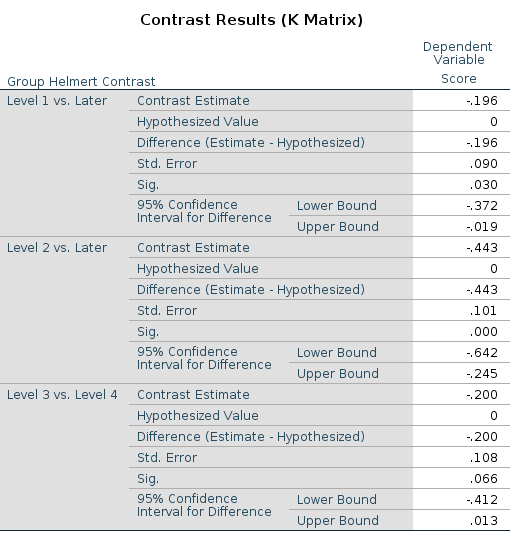
This is the LMATRIX one gets in SPSS

and this is the contrast matrix one gets from emmeans:

library(emmeans)
model<-lm(Score~Group,data=dat)
emm<-emmeans(model,~Group)
cont<-contrast(emm,"consec",reverse=T,adjust = "none")
coef(cont)
##        Group c.1 c.2 c.3
## Group1     1   1   0   0
## Group2     2  -1   1   0
## Group3     3   0  -1   1
## Group4     4   0   0  -1

When it comes to R model estimation ( lm(), lmer(), glm() ), however, we should notice that to obtain the same comparisons obtained by the other packages, one needs to code the comparisons in form of the model matrix, not the contrast matrix. This may be confusing, but that’s the way it is.

In fact, upon inspecting the coding scheme generated by the contr.* functions, one see that the coding does not correspond to the contrast matrix seen before.

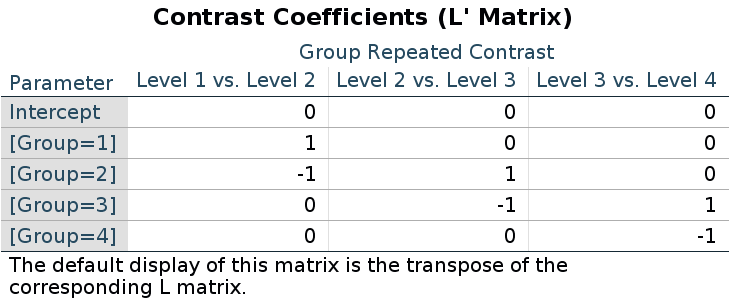
For repeated contrasts in R we use:

(-1)*contr.sdif(4)
##     2-1  3-2   4-3
## 1  0.75  0.5  0.25
## 2 -0.25  0.5  0.25
## 3 -0.25 -0.5  0.25
## 4 -0.25 -0.5 -0.75

Recall (cf. the repeated contrast results above) that the results are identical between the R, SPSS and emmeans, even thought the coding seems different.

Now, if you try to use the SPSS LMATRIX in R, you are not going to get the results expected by the repeated contrast. Indeed (coefficients were .100,-.344,-.200) :

ones<-matrix(c(1,-1,0,0,0,1,-1,0,0,0,1,-1),ncol=3)
ones
##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]   -1    1    0
## [3,]    0   -1    1
## [4,]    0    0   -1
contrasts(dat$Group)<-ones
summary(model)
## 
## Call:
## lm(formula = Score ~ Group, data = dat)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.06311 -0.27955 -0.00111  0.28531  1.65733 
## 
## Coefficients:
##             Estimate Std. Error t value  Pr(>|t|)    
## (Intercept)  0.15619    0.03936   3.969  0.000107 ***
## Group1      -0.19553    0.08959  -2.183  0.030477 *  
## Group2      -0.44344    0.10075  -4.402 0.0000192 ***
## Group3      -0.19956    0.10770  -1.853  0.065681 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.5109 on 166 degrees of freedom
## Multiple R-squared:  0.1473, Adjusted R-squared:  0.1319 
## F-statistic: 9.557 on 3 and 166 DF,  p-value: 0.000007399

The reason of this discrepancy is that the LMATRIX is the contrast matrix, a matrix that shows the linear hypotheses implied by the contrast and represents the starting point of the coding system, not the model matrix itself. Thus, the constrast matrix (SPSS LMATRIX) is useful to understand what is going on in the comparisons: by inspecting the contrast matrix one can easily see that in column 1 groups 1 and 2 are compared, in column 2 groups 2 vs 3, and so on.

A clear technical explanation is provided in Venables 2017, where you find the definition of the contrast matrix (\(C\) in the Venable’s vignette) and the model matrix (\(B\) in the vignette).

Ok, but what is the relation between the contrast matrix and the R model matrix? or even better: How do I get from the contrast matrix to the R model matrix? Just take the inverse of the contrast matrix and traspose it. In R, one can take the inverse of a matrix by using MASS::ginv() function. Let’s see:

##### SPSS LMATRIX ####
ones
##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]   -1    1    0
## [3,]    0   -1    1
## [4,]    0    0   -1
### take the inverse ####
iones<-ginv(ones)
### transpose it ###
t(iones)
##       [,1] [,2]  [,3]
## [1,]  0.75  0.5  0.25
## [2,] -0.25  0.5  0.25
## [3,] -0.25 -0.5  0.25
## [4,] -0.25 -0.5 -0.75

and there you are: the R model matrix.

Does it work in general? Yes! Take deviation contrast, with group 1 omitted.

SPSS LMATRIX is:

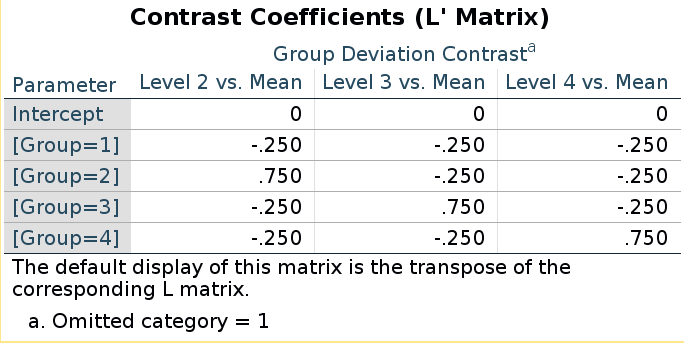
and R model matrix we have seen before:

(deviation<-matrix(rev(contr.sum(4)),ncol=3))
##      [,1] [,2] [,3]
## [1,]   -1   -1   -1
## [2,]    1    0    0
## [3,]    0    1    0
## [4,]    0    0    1

They seem different, but taking the inverse of the LMATRIX and transposing it, we get the R coding system.

##### SPSS LMATRIX ####
lmat<-matrix(rep(-.25,12),ncol=3)
lmat[2,1]<-.75
lmat[3,2]<-.75
lmat[4,3]<-.75
lmat
##       [,1]  [,2]  [,3]
## [1,] -0.25 -0.25 -0.25
## [2,]  0.75 -0.25 -0.25
## [3,] -0.25  0.75 -0.25
## [4,] -0.25 -0.25  0.75
### take the inverse ####
ilmat<-ginv(lmat)
### transpose it ###
round(t(ilmat),digits = 3)
##      [,1] [,2] [,3]
## [1,]   -1   -1   -1
## [2,]    1    0    0
## [3,]    0    1    0
## [4,]    0    0    1

There you have the actual model matrix.

Let us be sure and check polynomial contrasts.

SPSS LMATRIX is:

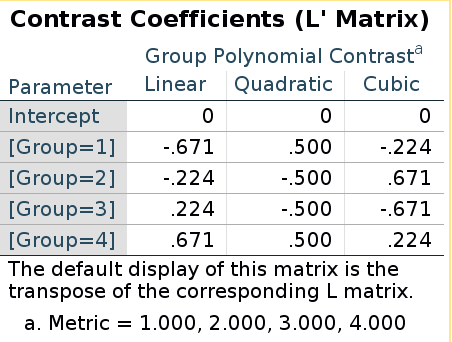
R model matrix:

(polynom<-contr.poly(4))
##              .L   .Q         .C
## [1,] -0.6708204  0.5 -0.2236068
## [2,] -0.2236068 -0.5  0.6708204
## [3,]  0.2236068 -0.5 -0.6708204
## [4,]  0.6708204  0.5  0.2236068

They are the same this time! Does it means that in this case the “inversion” does not apply? Well, it does apply, but because the polynomial contrast codes are orthogonal, the inverse of the contrast matrix is equal to the transpose of the contrast matrix, thus taking the inverse and then transpose it gives back the same matrix (cf orthogonal matrix)

ipoly<-ginv(polynom)
t(ipoly)
##            [,1] [,2]       [,3]
## [1,] -0.6708204  0.5 -0.2236068
## [2,] -0.2236068 -0.5  0.6708204
## [3,]  0.2236068 -0.5 -0.6708204
## [4,]  0.6708204  0.5  0.2236068

Building custom contrast in emmeans

We have seen that emmeans allows to define custom contrast coding. When we do that, we should remember that we need to define the contrast matrix, not the model matrix. Thus, for repeated contrast, in R we used (-1)*contr.sdif(n):

(rcodes<-(-1)*contr.sdif(4))
##     2-1  3-2   4-3
## 1  0.75  0.5  0.25
## 2 -0.25  0.5  0.25
## 3 -0.25 -0.5  0.25
## 4 -0.25 -0.5 -0.75

and emmeans uses:

cont<-contrast(emm,"consec",referse=T,adjust = "none")
(weigths<-coef(cont)[,2:4])
##        c.1 c.2 c.3
## Group1  -1   0   0
## Group2   1  -1   0
## Group3   0   1  -1
## Group4   0   0   1

To get the contrast matrix from the model matrix we neet to get the inverse of the transpose:

#### model matrix ######
rcodes
##     2-1  3-2   4-3
## 1  0.75  0.5  0.25
## 2 -0.25  0.5  0.25
## 3 -0.25 -0.5  0.25
## 4 -0.25 -0.5 -0.75
#### transpose the R model matrix ######
tcodes<-t(rcodes)
#### invert it #####
round(ginv(tcodes),digits = 3)
##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]   -1    1    0
## [3,]    0   -1    1
## [4,]    0    0   -1

Now we can build a custom contrast function for emmeans: let’s do helmert as we defined above.

Let’s start with the model matrix used in R.

con_weights<-matrix(rev(contr.helmert(4)),ncol=3)
cv<-apply(con_weights,2,max)+1
diag_cv<-matrix(rep(cv,each=4),ncol=3)
helm<-con_weights/diag_cv
helm
##       [,1]       [,2] [,3]
## [1,]  0.75  0.0000000  0.0
## [2,] -0.25  0.6666667  0.0
## [3,] -0.25 -0.3333333  0.5
## [4,] -0.25 -0.3333333 -0.5

Take the inverse of the transpose of it

(contr_mat<-ginv(t(helm)))
##            [,1]                       [,2]
## [1,]  1.0000000 -0.00000000000000006343273
## [2,] -0.3333333  1.00000000000000000000000
## [3,] -0.3333333 -0.50000000000000011102230
## [4,] -0.3333333 -0.50000000000000011102230
##                           [,3]
## [1,] -0.0000000000000001098687
## [2,] -0.0000000000000001256066
## [3,]  0.9999999999999995559108
## [4,] -0.9999999999999997779554

This is the contrast matrix we can pass to emmeans. We just need to wrap it up in a function with .emmc() reference class and levels as input.

helmert.emmc<<-function(levs,wts) {
  n<-length(levs)
  con_weights<-matrix(rev(contr.helmert(n)),ncol=n-1)
  cv<-apply(con_weights,2,max)+1
  diag_cv<-matrix(rep(cv,each=n),ncol=n-1)
  helm<-con_weights/diag_cv
  model_mat<-ginv(t(helm))
  M <- as.data.frame(model_mat)
  names(M) <- paste(levs[1:(length(levs)-1)],"vs subsequent")
  attr(M, "desc") <- "Helmert contrasts"
  M
}
helmert.emmc(levels(dat$Group))
##   1 vs subsequent            2 vs subsequent
## 1       1.0000000 -0.00000000000000006343273
## 2      -0.3333333  1.00000000000000000000000
## 3      -0.3333333 -0.50000000000000011102230
## 4      -0.3333333 -0.50000000000000011102230
##             3 vs subsequent
## 1 -0.0000000000000001098687
## 2 -0.0000000000000001256066
## 3  0.9999999999999995559108
## 4 -0.9999999999999997779554
contrast(emm,"helmert",adjust="none")
##  contrast             estimate     SE  df t.ratio p.value
##  Group1 vs subsequent   -0.196 0.0896 166  -2.183  0.0305
##  Group2 vs subsequent   -0.443 0.1007 166  -4.402  <.0001
##  Group3 vs subsequent   -0.200 0.1077 166  -1.853  0.0657

and we get the contrast estimates as expected. For the difference contrast we can use con_weights<-contr.helmert(n) in the function and we get the correct codes.

Comments?

Got comments, issues or spotted a bug? Please open an issue on GAMLj at github or send me an email