keywords jamovi, R, Mixed Models, Multilevel Models, Nested design, Nested levels

GAMLj version ≥ 1.0.0

Issue

I have nested clustering variables (nested levels) and I am not sure the model is considering the nesting correctly.

Short answer

Be sure that every cluster, at each level, has a unique value (factor level). If so, the model considers the nesting correctly

Long answer

Introduction

Mixed models are often used to analyze multilevel designs, in which several clustering variables appear. When more than one clustering variable exists, clusters can be nested or cross-classified. See Mixed Models: Subjects by Stimuli random effects for some examples. In case of nested models, users sometimes wonder how to signal to GAMLj that the clustering variables are nested, meaning that they define different levels of a multilevel design. This uncertainty is often supported by the fact that lmer() command of R package lme4 seems to require specifying the nested nature of the clustering variables with special notation (see below). However, this is not the case. Nested clustering can be specified both in lmer() command and in GAMLj without any special notation (model formula notation), and the models are correctly estimated taking into the account the nested nature of the design. Let’s see a toy example to clarifying the issue.

A quick three-level example

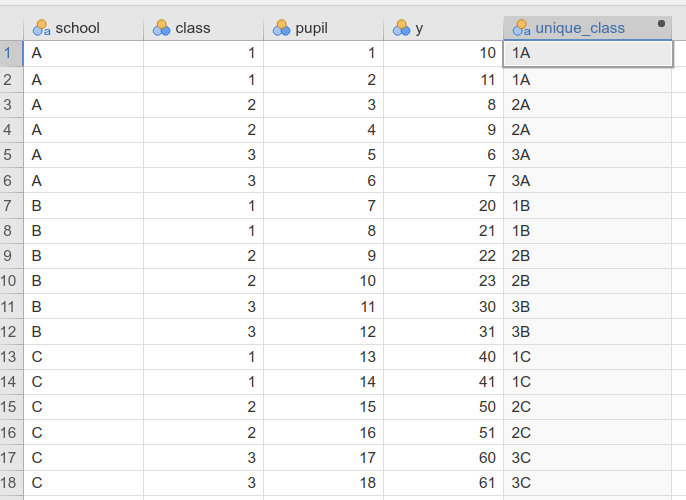
Assume you have three schools, within each school three classes, and pupils within classes. Schools are coded in variable school as A, B, and C. Assume you coded, within each school, the three classes as 1, 2, and 3. Your dataset will look like this.

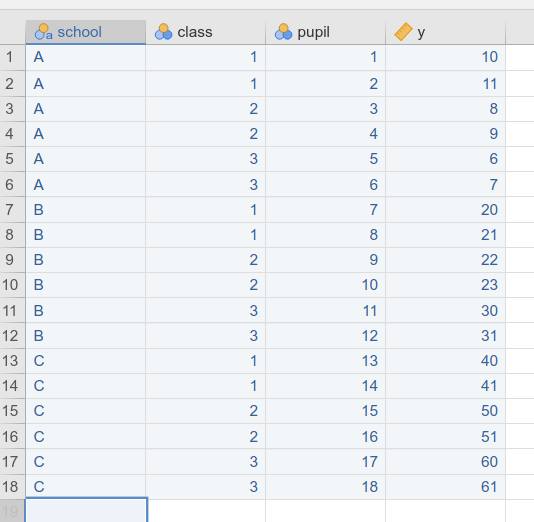
This means that the design features 3 schools, and 9 classes. Usually, you want to estimate the random coefficients (in this simple case only the intercepts) across schools and classes. If you run a model in GAMLj using these data, however, the model will pool together all pupils in class 1, all pupils in class 2 an so on, irrespective of their school, as if pupils of different schools belonged to the same class. Indeed, in GAMLj you would have 3 schools and 3 classes :

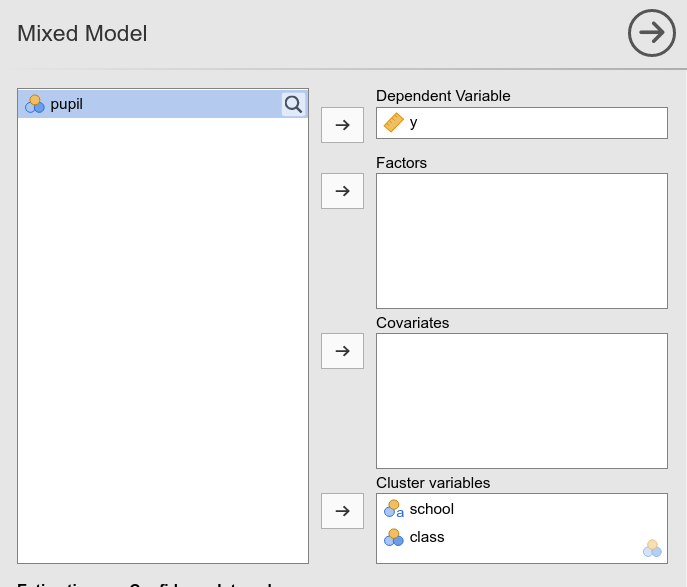
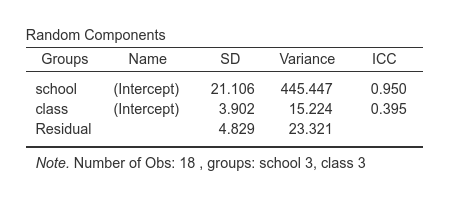
This is equivalent to run in R lme4 command

library(lmerTest)
data$school<-factor(data$school)
data$class<-factor(data$class)
mod<-lmer(y~1+(1|school)+(1|class),data=data)
print(mod,digits=5)
## Linear mixed model fit by REML ['lmerModLmerTest']
## Formula: y ~ 1 + (1 | school) + (1 | class)
##    Data: data
## REML criterion at convergence: 117
## Random effects:
##  Groups   Name        Std.Dev.
##  school   (Intercept) 21.1056 
##  class    (Intercept)  3.9018 
##  Residual              4.8291 
## Number of obs: 18, groups:  school, 3; class, 3
## Fixed Effects:
## (Intercept)  
##      27.833

Solution

To avoid this issue, R lmer() allows using a different notation to specify the nesting. Namely

mod<-lmer(y~1+(1|school/class),data=data)
print(mod,digits=5)
## Linear mixed model fit by REML ['lmerModLmerTest']
## Formula: y ~ 1 + (1 | school/class)
##    Data: data
## REML criterion at convergence: 87.6
## Random effects:
##  Groups       Name        Std.Dev.
##  class:school (Intercept)  6.6144 
##  school       (Intercept) 20.8497 
##  Residual                  0.7071 
## Number of obs: 18, groups:  class:school, 9; school, 3
## Fixed Effects:
## (Intercept)  
##      27.833

As you can see, the model has now 9 classes and 3 schools, as intended. However, the only thing that this notation does is to build a new variable class:school which assigns unique values to each class. Indeed, we can do that in R and in GAMLj to obtain exactly the same results.

In R:

data$unique_class<-apply(cbind(data$class,data$school),1,paste,collapse="_")
data$unique_class<-factor(data$unique_class)

mod<-lmer(y~1+(1|school)+(1|unique_class),data=data)
print(mod,digits=5)
## Linear mixed model fit by REML ['lmerModLmerTest']
## Formula: y ~ 1 + (1 | school) + (1 | unique_class)
##    Data: data
## REML criterion at convergence: 87.6
## Random effects:
##  Groups       Name        Std.Dev.
##  unique_class (Intercept)  6.6144 
##  school       (Intercept) 20.8497 
##  Residual                  0.7071 
## Number of obs: 18, groups:  unique_class, 9; school, 3
## Fixed Effects:
## (Intercept)  
##      27.833

In jamovi:

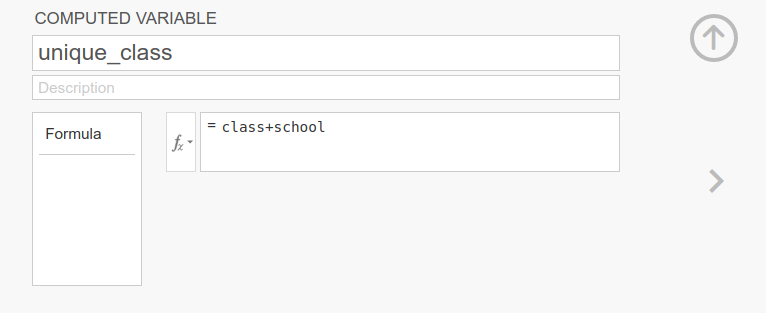
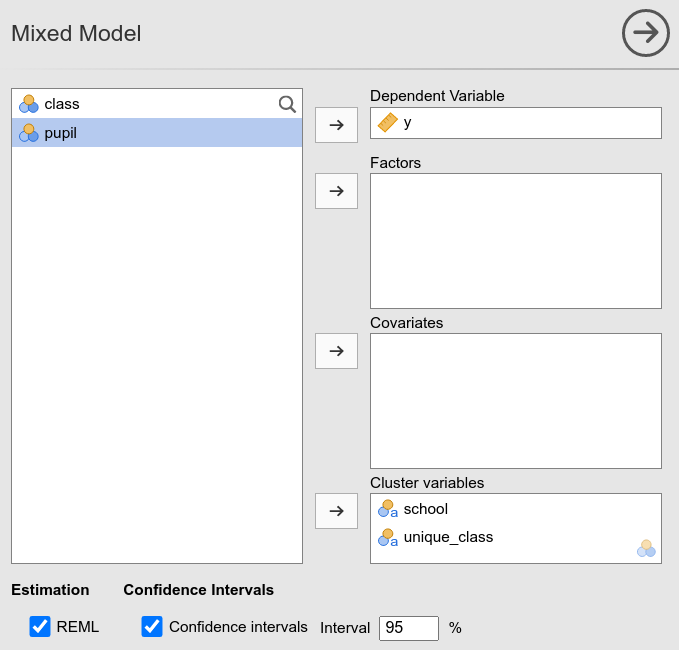
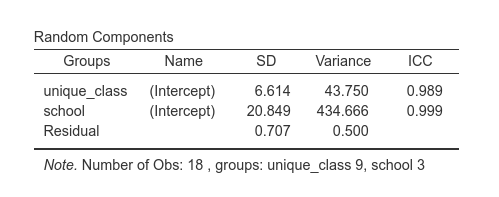
Indeed, the new variable unique_class is simply assigning unique values to the classes.

Recap

When dealing with nested levels, be sure that each group (cluster) is coded with a unique code, and the nesting structure will be automatically taken into the account by the model.

Rosetta’s files

Comments?

Got comments, issues or spotted a bug? Please open an issue on GAMLj at github or send me an email