General Linear Model
General Linear Model module of the GAMLj suite for jamovi
GAMLj version ≥ 2.6.0
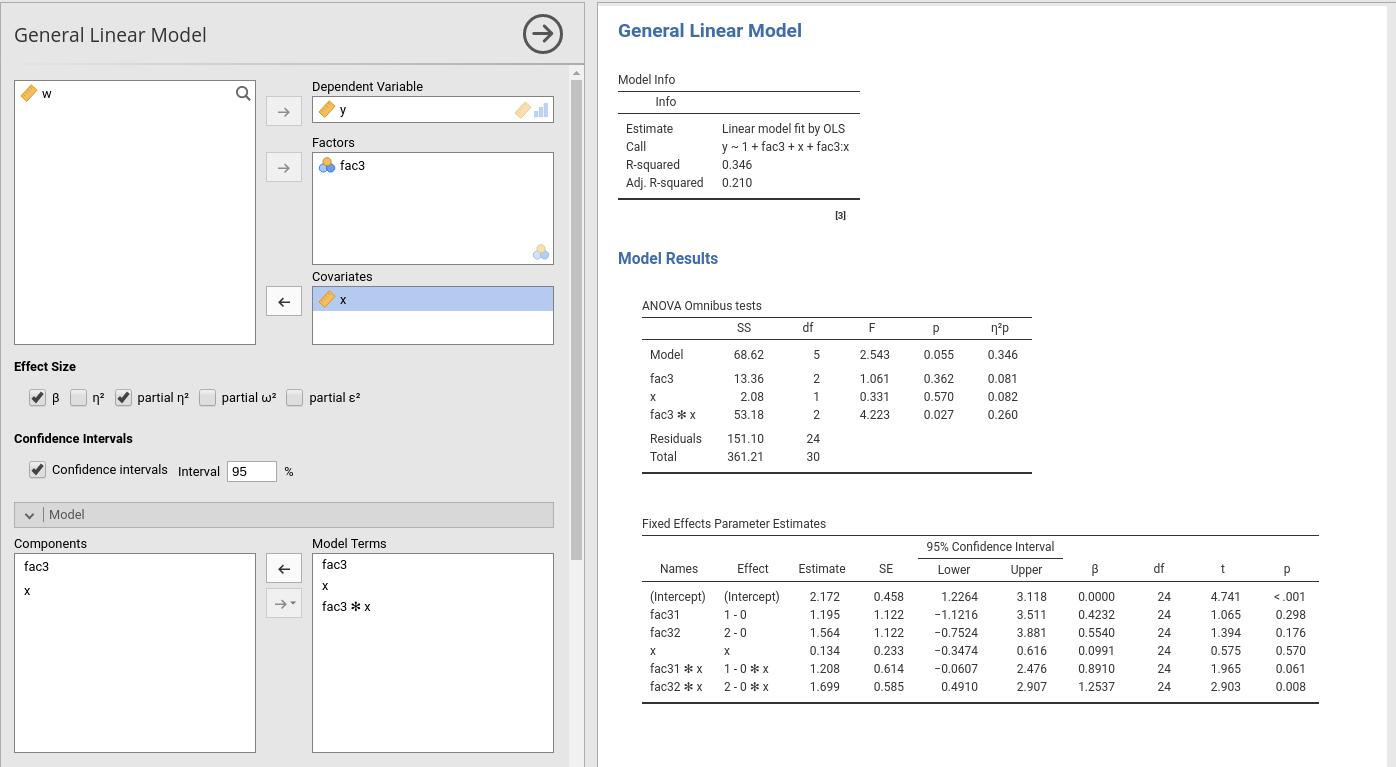
The module estimates a general linear model with categorical and/or continuous variables, with options to facilitate estimation of interactions, simple slopes, simple effects, etc.
Module
The module can estimate OLS linear models for any combination of categorical and continuous variables, thus providing an easy way for multiple regression, ANOVA, ANCOVA and moderation analysis.
Estimates
The module provides ANOVA tables and parameters estimates for any estimated model. Effect size indices (eta, partial eta, partial omega, partial epsilon, and beta) are optionally computed.
Variables definition follows jamovi standards, with categorical independent variables defined in Factors and continuous independent variables in Covariates.
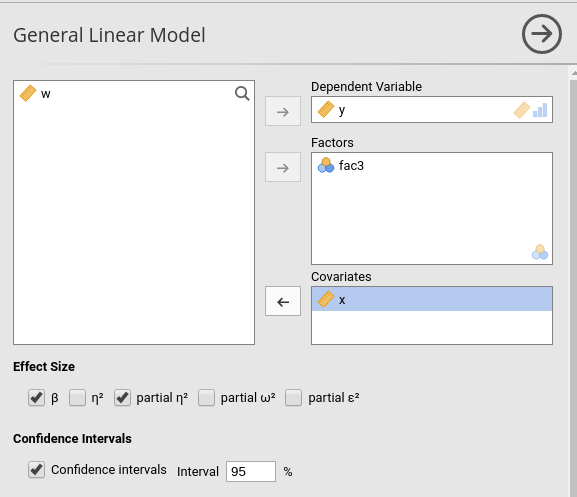
Effect size indices are optionally computed by selecting the following options (see Details: GLM effect size indices):
- \(\beta\) : standardized regression coefficients
- \(\eta^2\): (semi-partial) eta-squared
- \(\eta^2\)p : partial eta-squared
- \(\omega^2\) : omega-squared
- \(\omega^2\)p : partial omega-squared
- \(\epsilon^2\) : epsilon-squared
- \(\epsilon^2\)p : partial epsilon-squared
Confidence intervals of the parameters can be also selected in Options tab.
Please check the details in Details: GLM effect size indices
Model
By default, the model terms are filled in automatically for main effects and for interactions with categorical variables.
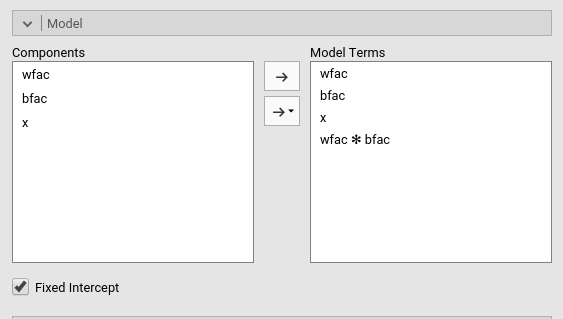
Interactions between continuous variables or categorical and continuous variables can be set by clicking the second arrow icon.
Polinomial effects for continuous variables can be added to the model. When a variable is selected in the Components field, a little number appears on the right side of the selection. The number indicates the order of the effect.
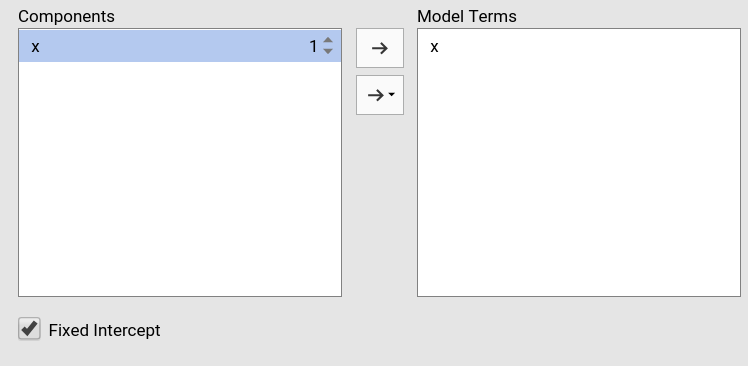
By increasing that number before dragging the term into the Model Terms field, one can include any high order effect.
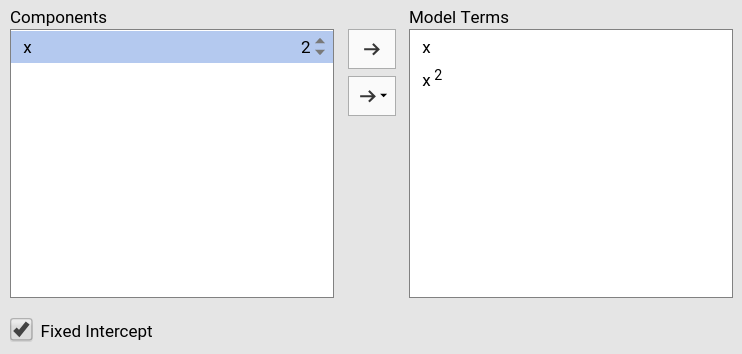
Increasing the order number and combining the selection with other variables allows including interactions involving higher order effects of a variable.
The option Fixed Intercept includes an intercept in the model. Unflag it to estimate zero-intercept models (Regression through the origin, but see here before you do it ).
Factors coding

It allows to code the categorical variables according to different coding schemas. The coding schema applies to all parameters estimates. The default coding schema is simple, which is centered to zero and compares each means with the reference category mean. The reference category is the first appearing in the variable levels.
Note that all contrasts but dummy guarantee to be centered to zero (intercept being the grand mean), so when involved in interactions the other variables coefficients can be interpret as (main) average effects. If contrast dummy is set, the intercept and the effects of other variables in interactions are estimated for the first group of the categorical IV.
Contrasts definitions are provided in the estimates table. More detailed definitions of the comparisons operated by the contrasts can be obtained by selecting Show contrast definition table.
Differently to standard R naming system, contrasts variables are always named with the name of the factor and progressive numbers from 1 to K-1, where K is the number of levels of the factor.
In reading the contrast labels, one should interpret the
(1,2,3) code as meaning “the mean of the levels 1,2, and 3
pooled toghether”. If factor levels 1,2 and 3 are all levels of the
factor in the samples, (1,2,3) is equivalent to “the mean
of the sample”. For example, for a three levels factor, a contrast
labeled 1-(1,2,3) means that the contrast is comparing the
mean of level 1 against the mean of the sample. For the same factor, a
contrast labeled 1-(2,3) indicates a comparison between
level 1 mean and the subsequent levels means pooled together.
More details and examples Rosetta store: contrasts.
Covariates Scaling
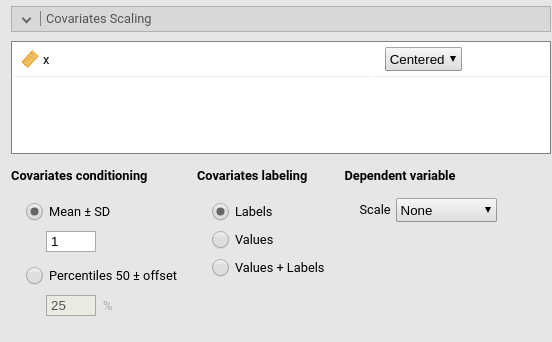
Continuous variables can be centered, standardized (z-scores), log-transformed (Log) or used as they are (none). The default is centered because it makes our lives much easier when there are interactions in the model, and do not affect the B coefficients when there are none. Thus, if one is comparing results with other software that does not center the continuous variables, without interactions in the model one would find only a discrepancy in the intercept, because in GAMLj the intercept represents the expected value of the dependent variable for the average value of the independent variable. If one needs to unscale the variable, simply select none.
Covariates conditioning rules how the model is conditioned to different values of the continuous independent variables in the simple effects estimation and in the plots when there is an interaction in the model.
Mean+SD: means that the IV is conditioned to the \(mean\), to \(mean+k \cdot sd\), and to \(mean-k\cdot sd\), where \(k\) is ruled by the white field below the option. Default is 1 SD.
Percentile 50 +offset: means that the IV is conditioned to the \(median\), the \(median+k P\), and the \(median-k\cdot P\), where \(P\) is the offset of percentile one needs. Again, the \(P\) is ruled by the white field below the option. Default is 25%. The default conditions the model to:
\(50^{th}-25^{th}=25^{th}\) percentile
\(50^{th}\) percentile
\(50^{th}+25^{th}=75^{th}\) percentile
The offset should be within 5 and 50.
Note that with either of these two options, one can estimate simple effects and plots for any value of the continuous IV.
Covariates labeling decides which label should be associated with the estimates and plots of simple effects as follows:
Labels produces strings of the form \(Mean \pm SD\)
Values uses the actual values of the variables
Labels+Values produces labels of the form \(Mean \pm SD=XXXX\), where
XXXXis the actual value.
The option Dependent variable scale allows to transform the dependent variable. The dependent variable can be centered, standardized (z-scores), log-transformed (Log) or used as they are (none). The default is none, so no transformation is applied.
Post-hocs

Post-hoc tests can be accomplished for the categorical variables groups by selecting the appropriated factor and flag the required tests
Post-hoc tests are implemented based on R package emmeans. All tecnical info can be found here
Plots
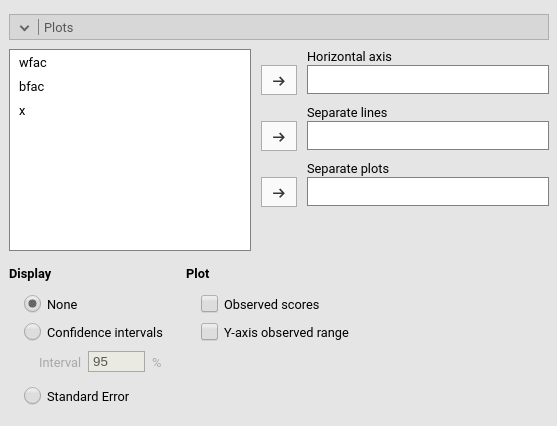
The “plots” menu allows for plotting main effects and interactions for any combination of types of variables, making it easy to plot interaction means plots, simple slopes, and combinations of them. The best plot is chosen automatically.
By filling in Horizontal axis one obtains the group means of the selected factor or the regression line for the selected covariate
By filling in Horizontal axis and Separated lines one obtains a different plot depending on the type of variables selected:
- Horizontal axis and Separated lines are both factors, one obtains the interaction plot of group means.
- Horizontal axis is a factor and Separated lines is a covariate. One obtains the plot of group means of the factor estimated at three different levels of the covariate. The levels are decided by the Covariates conditioning options above.
- Horizontal axis and Separated lines are covariates. One obtains the simple slopes graph of the simple slopes of the variable in horizontal axis estimated at three different levels of the covariate.
By filling in Separate plots one can
probe three-way interactions. If the selected variable is a factor, one
obtains a two-way graph (as previously defined) for each level of the
“Separate plots” variable. If the selected variable is a covariate, one
obtains a two-way graph (as previously defined) for the
Separate plots variable centered to conditioning values
selected in the Covariates conditioning
options.
Flagging the Display options add Confidence intervals (or confidence bands) or Standard errors to the plots.
Plot options allows to add observed data
to the plot (Observed scores) or to fix the
range of the plot to the actual range of the dependent variable (Y-axis observed range), without the need to plot
the actual predicted values. When Separate plots are
required, in each plot are showed only the observed scores of the
moderator level for which the plot is done when the moderator is a
categorical one, otherwise all data are plot in each plot.
Estimated marginal means
Print the estimate expected means, SE, df and confidence intervals of the precicted dependent variable by factors in the model. When `Include covariates is selected, factors levels are crossed also with the conditiong levels of the continuous variables (if any). The conditioning values are selected in Covariates Scaling panel.
Assumptions checks
Homogeneity tests provides Levene’s test for equal variances across groups defined by factors (homoschedasticity).
Test normality of residuals provides Kolmogorov-Smirnov and Shapiro-Wilk tests for normality of residuals.
Q-Q plot of residuals outputs a Q-Q plot (observed residual quantiles on expected residual quantiles). More general info here
Residuals histogram outputs the histogram of the distribution of the residuals, with an overlaying ideal normal distribution with mean and variance equal to the residuals distribution parameters.
Residuals-Predicted plot produces a scatterplot with the residuals on the Y-axis and the predicted in the X-axis. It can be usufull to assess heteroschdasticity.
Options
Additional options that do not fit elsewhere.
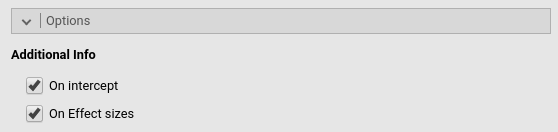
Additional Info- On intercept_ provides effect size for the intercept
- On Effect sizes: outputs a new table with all effect sizes available, with confidence intervals
- see Details: GLM effect size indices
Examples
Some worked out examples of the analyses carried out with jamovi GAMLj are posted here (more to come)
Details
Some more information about the module specs can be found here # Specs
Comments?
Got comments, issues or spotted a bug? Please open an issue on GAMLj at github or send me an email
’